The foundation is assumed to be elastic and is simulated by an edge expansion (see Appendix Image 3).
The properties of the elements (foundation elements or Vogt elements) within this expansion are determined as follows:
Based on Boussinesq’s formula for an elastic half-space, Vogt calculated the shifts with regard to a norm force N, shear force Q, and momentum M distributed over a surface b x t of the plane surface of the half-space (see Fig. 1).
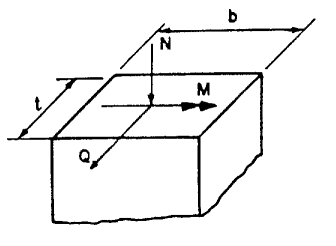
Fig. 1 Stress net force of the surface b*t on the elastic half-space
After a small change to the notations in Vogts relations between the cutting forces (N, Q, M) and the mean displacements (vN, vQ, vM) gives the following:
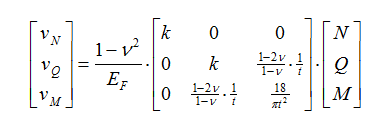 (1)
(1)EF signifies therein the modulus of elasticity of the foundation, Poisson's ratio, and k is a coefficient varied at the ratio of b/t (current values of k are found between 2.25 and 3.00).
Fig. 2 Cantilever plate stressed by cutting forces.
The flexibility matrix with regards to the cantilever plate in Fig. 2, which is stressed by the three cutting forces N, Q, and M and which matches the matrix (1) can be described as fol-lows:
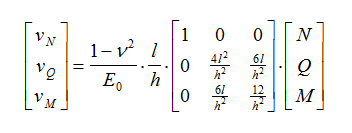 (2)
(2)DTherein E0 signifies the modulus of elasticity of the cantilever plate. There are three adjust-ment variables E0, l, and h in Matrix (2) to best match matrix (1). The component vQ, in rela-tion to Q can generally be neglected as emphasised by Vogt.
In all practise-oriented cases, this component is actually much smaller than the component for M. The adjustment of the central matrix element is therefor negligible. The three variables can be utilised to correct the three remaining matrix elements.
For = 0 and k = 2.5 results in the following corrections:
- h = 2.300 t (=115 m for Karakaya under 600 m.a.s.l.)
- l = 0.350 t (=17.5 m for Karakaya under 600 m.a.s.l.))
- E0= 0.061 EF (=10.98 kp/cm2 for Karakaya)
There is a good correlation between the displacements calculated using this method and the measurements from existing dams.